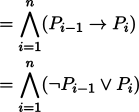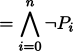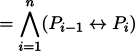zantufa jonma'o smuni

banjubu'o / français / 日本語 / English

Semantics of forethought logical connectives

The forethought connectives of Zantufa that is a series of parsers for unofficial Lojban are much more expressive than those of official grammar.

Zantufa is syntactic parser, and it does not fix rules for sematics by itself, though.

Here is only a suggestion of semantics of the forethought logical connectives in order to gain profit from expressiveness of Zantufa grammar.

The sentences in Lojban here follow the grammar of Zantufa_1.16.

List of symbols used on this page

Symbol	Definition
¬P	na ku P
P ∨ Q	P i ja Q
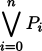
	((((P0 ∨ P1) ∨ P2) ∨ ...) ∨ Pn)
P ∧ Q	P i je Q
	((((P0 ∧ P1) ∧ P2) ∧ ...) ∧ Pn)
P ↔ Q	P i jo Q
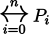
	((((P0 ↔ P1) ↔ P2) ↔ ...) ↔ Pn)
P ⊕ Q	P i jonai Q
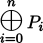
	((((P0 ⊕ P1) ⊕ P2) ⊕ ...) ⊕ Pn)
P ⊏ Q	P i ju Q
	((((P0 ⊏ P1) ⊏ P2) ⊏ ...) ⊏ Pn) = P0
P ⊐ Q	P i se ju Q
	((((P0 ⊐ P1) ⊐ P2) ⊐ ...) ⊐ Pn) = Pn

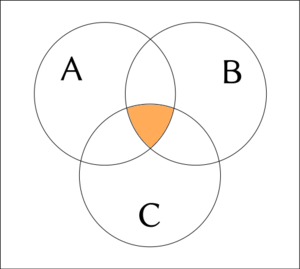
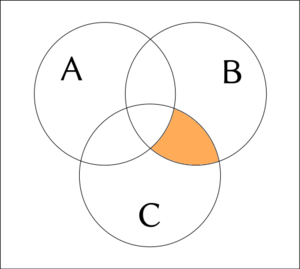
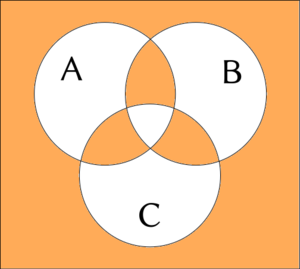
In the following explanation, examples for 3-ary or 4-ary connection are sometimes accompanied with a truth value table. The falseness is represented by 0; the truth is represented by 1.

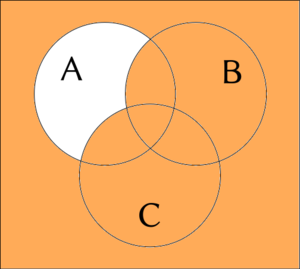
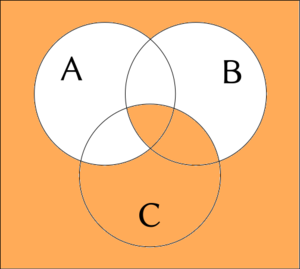
Examples for 3-ary connection are sometimes accompanied with a Venn diagram. White color represents falseness; orange color represents truth.

ga

ga A gi B gi C gi ...

Definition

ga P0 gi P1 gi ... gi Pn (gi'i)

=

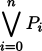
Example

3-ary case: {ga A gi B gi C}=(A∨B)∨C

ga zei ven

A	B	C	A∨B	(A∨B)∨C
1	1	1	1	1
0	1	1	1	1
1	0	1	1	1
0	0	1	0	1
1	1	0	1	1
0	1	0	1	1
1	0	0	1	1
0	0	0	0	0

ga bo A gi B gi C gi ...

Definition

	ga bo P0 gi P1 gi ... gi Pn (gi'i)
=	ga P0 gi P1 gi ... gi Pn (gi'i)
=

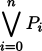
ga nai A gi B gi C gi ...

Definition

	ga nai P0 gi P1 gi ... gi Pn (gi'i)
=	ga ¬P0 gi P1 gi ... gi Pn (gi'i)

Example

3-ary case: {ga nai A gi B gi C}=(¬A∨B)∨C

ga zei nai zei ven

A	B	C	¬A∨B	(¬A∨B)∨C
1	1	1	1	1
0	1	1	1	1
1	0	1	0	1
0	0	1	1	1
1	1	0	1	1
0	1	0	1	1
1	0	0	0	0
0	0	0	1	1

ga nai bo A gi B gi C gi ...

Definition

ga nai bo P0 gi P1 gi ... gi Pn (gi'i)

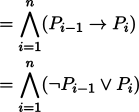
Example

3-ary case:

	{ga nai bo A gi B gi C}
=	((A→B)∧(B→C))
=	((¬A∨B)∧(¬B∨C))

ga zei nai zei bo zei ven

A	B	C	¬A∨B	¬B∨C	(¬A∨B)∧(¬B∨C)
1	1	1	1	1	1
0	1	1	1	1	1
1	0	1	0	1	0
0	0	1	1	1	1
1	1	0	1	0	0
0	1	0	1	0	0
1	0	0	0	1	0
0	0	0	1	1	1

Difference

{ga nai bo A gi B gi C} ≠ {A i na ja B i na ja C}

	A i na ja B i na ja C
=	(A → B) → C
=	¬(¬A ∨ B) ∨ C

i zei na zei ja zei ven

A	B	C	¬A∨B	¬(¬A∨B)∨C
1	1	1	1	1
0	1	1	1	1
1	0	1	0	1
0	0	1	1	1
1	1	0	1	0
0	1	0	1	0
1	0	0	0	1
0	0	0	1	0

ge

ge A gi B gi C gi ...

Definition

	ge P0 gi P1 gi ... gi Pn (gi'i)
=

Example

3-ary case: {ge A gi B gi C}=(A∧B)∧C

ge zei ven

A	B	C	A∧B	(A∧B)∧C
1	1	1	1	1
0	1	1	0	0
1	0	1	0	0
0	0	1	0	0
1	1	0	1	0
0	1	0	0	0
1	0	0	0	0
0	0	0	0	0

ge bo A gi B gi C gi ...

Definition

	ge bo P0 gi P1 gi ... gi Pn (gi'i)
=	ge P0 gi P1 gi ... gi Pn (gi'i)
=

ge nai A gi B gi C gi ...

Definition

	ge nai P0 gi P1 gi ... gi Pn (gi'i)
=	ge ¬P0 gi P1 gi ... gi Pn (gi'i)

Example

3-ary case: {ge nai A gi B gi C}=(¬A∧B)∧C

ge zei nai zei ven

A	B	C	¬A∧B	(¬A∧B)∧C
1	1	1	0	0
0	1	1	1	1
1	0	1	0	0
0	0	1	0	0
1	1	0	0	0
0	1	0	1	0
1	0	0	0	0
0	0	0	0	0

ge nai bo A gi B gi C gi ...

Definition

ge nai bo P0 gi P1 gi ... gi Pn (gi'i)

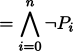
Example

3-ary case:

	{ge nai bo A gi B gi C}
=	{ge nai A gi nai B gi nai C}
=	{A i na je nai B i je nai C}
=	(¬A∧¬B)∧¬C

ge zei nai zei bo zei ven

A	B	C	¬A∧¬B	(¬A∧¬B)∧¬C
1	1	1	0	0
0	1	1	0	0
1	0	1	0	0
0	0	1	1	0
1	1	0	0	0
0	1	0	0	0
1	0	0	0	0
0	0	0	1	1

go

go A gi B gi C gi ...

Definition

	go P0 gi P1 gi ... gi Pn (gi'i)
=

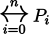
Example

3-ary case: {go A gi B gi C}=(A↔B)↔C

go zei ven

A	B	C	A↔B	(A↔B)↔C
1	1	1	1	1
0	1	1	0	0
1	0	1	0	0
0	0	1	1	1
1	1	0	1	0
0	1	0	0	1
1	0	0	0	1
0	0	0	1	0

go bo A gi B gi C gi ...

Definition

go bo P0 gi P1 gi ... gi Pn (gi'i)

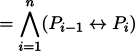
Example

3-ary case:

	{go bo A gi B gi C}
=	((A↔B)∧(B↔C))

go zei bo zei ven

A	B	C	A↔B	B↔C	(A↔B)∧(B↔C)
1	1	1	1	1	1
0	1	1	0	1	0
1	0	1	0	0	0
0	0	1	1		0
1	1	0	1	0	0
0	1	0	0	0	0
1	0	0	0	1	0
0	0	0	1	1	1

go nai A gi B gi C gi ...

Definition

	go nai P0 gi P1 gi ... gi Pn (gi'i)
=	go ¬P0 gi P1 gi ... gi Pn (gi'i)

Example

3-ary case: {go nai A gi B gi C}=(¬A↔B)↔C

go zei nai zei ven

A	B	C	¬A↔B	(¬A↔B)↔C
1	1	1	0	0
0	1	1	1	1
1	0	1	1	1
0	0	1	0	0
1	1	0	0	1
0	1	0	1	0
1	0	0	1	0
0	0	0	0	1

go nai bo A gi B gi C gi ...

Definition

It is defined recursively as follows.

2-ary case of P₀ and P₁:

	go nai bo P0 gi P1 (gi'i)
=	go nai P0 gi P1 (gi'i)
=	P0 ⊕ P1
=	¬P0 ↔ P1

3-ary case of P₀, ... , P_n (n≥2):

	go nai bo P0 gi ... gi Pn (gi'i)
=	((go nai bo P0 gi ... gi Pn-1 (gi'i)) ⊕ Pn) ∧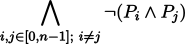

Example

3-ary case:

	{go nai bo A gi B gi C}
=	((go nai A gi B) ⊕ C) ∧ ¬(A∧B)
=	((A⊕B)⊕C) ∧ ¬(A∧B)

go zei nai zei bo zei ven

A	B	C	A⊕B	(A⊕B)⊕C	¬(A∧B)	((A⊕B)⊕C) ∧ ¬(A∧B)
1	1	1	0	1	0	0
0	1	1	1	0	1	0
1	0	1	1	0	1	0
0	0	1	0	1	1	1
1	1	0	0	0	0	0
0	1	0	1	1	1	1
1	0	0	1	1	1	1
0	0	0	0	0	1	0

4-ary case:

	{go nai bo A gi B gi C gi D}
=	((go nai bo A gi B gi C) ⊕ D) ∧ ¬(A∧B) ∧ ¬(B∧C) ∧ ¬(C∧A)

A	B	C	D	go nai bo A gi B gi C	(go nai bo A gi B gi C) ⊕ D	¬(A∧B)	¬(B∧C)	¬(C∧A)	((go nai bo A gi B gi C) ⊕ D) ∧ ¬(A∧B) ∧ ¬(B∧C) ∧ ¬(C∧A)
1	1	1	1	0	1	0	0	0	0
0	1	1	1	0	1	1	0	1	0
1	0	1	1	0	1	1	1	0	0
0	0	1	1	1	0	1	1	1	0
1	1	0	1	0	1	0	1	1	0
0	1	0	1	1	0	1	1	1	0
1	0	0	1	1	0	1	1	1	0
0	0	0	1	0	1	1	1	1	1
1	1	1	0	0	0	0	0	0	0
0	1	1	0	0	0	1	0	1	0
1	0	1	0	0	0	1	1	0	0
0	0	1	0	1	1	1	1	1	1
1	1	0	0	0	0	0	1	1	0
0	1	0	0	1	1	1	1	1	1
1	0	0	0	1	1	1	1	1	1
0	0	0	0	0	0	1	1	1	0

Difference

{go nai bo P₀ gi P₁ gi ... gi P_n (gi'i)} ≠ {P₀ i jo nai P₁ i jo nai ... i jo nai P_n}

Here is, for example, the table of truth value of connection by {i jo nai}. It is different from that of {go nai bo A gi B gi C gi D}.

	{A i jo nai B i jo nai C i jo nai D}
=	{A i na jo B i na jo C i na jo D}
=	((A ⊕ B) ⊕ C) ⊕ D

i zei jo zei nai zei ven

A	B	C	D	A ⊕ B	(A ⊕ B) ⊕ C	((A ⊕ B) ⊕ C) ⊕ D
1	1	1	1	0	1	0
0	1	1	1	1	0	1
1	0	1	1	1	0	1
0	0	1	1	0	1	0
1	1	0	1	0	0	1
0	1	0	1	1	1	0
1	0	0	1	1	1	0
0	0	0	1	0	0	1
1	1	1	0	0	1	1
0	1	1	0	1	0	0
1	0	1	0	1	0	0
0	0	1	0	0	1	1
1	1	0	0	0	0	0
0	1	0	0	1	1	1
1	0	0	0	1	1	1
0	0	0	0	0	0	0

gu

gu A gi B gi C gi ...

Definition

	gu P0 gi P1 gi ... gi Pn (gi'i)
=
=	P0

Example

3-ary case:

	{gu A gi B gi C}
=	(A ⊏ B) ⊏ C
=	A

gu zei ven

gu bo A gi B gi C gi ...

Definition

	gu bo P0 gi P1 gi ... gi Pn (gi'i)
=	gu P0 gi P1 gi ... gi Pn (gi'i)
=
=	P0

gu nai A gi B gi C gi ...

Definition

	gu nai P0 gi P1 gi ... gi Pn (gi'i)
=	gu ¬P0 gi P1 gi ... gi Pn (gi'i)
=	¬P0

Example

3-ary case:

	{gu nai A gi B gi C}
=	{gu ¬A gi B gi C}
=	¬A

gu zei nai zei ven

gu nai bo A gi B gi C gi ...

Definition

	gu nai bo P0 gi P1 gi ... gi Pn (gi'i)
	gu ¬P0 gi ¬P1 gi ... gi ¬Pn (gi'i)
=	¬P0
=	gu nai P0 gi P1 gi ... gi Pn (gi'i)

segu

se xi ky gu A gi B gi C gi ... (se gu, te gu, ve gu, xe gu, ..., se xi ro gu)

	se xi ky gu P0 gi P1 gi ... gi Pn (gi'i)
=	P0 i se ju P1 i se ju ... i se ju Pk 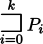i ju ... i ju Pn
=	i ju ... i ju Pn
=	Pk i ju ... i ju Pn
=
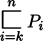
=	Pk

{se xi no gu}	=	{gu}
{se xi pa gu}	=	{se gu}
{se xi re gu}	=	{te gu}
{se xi ci gu}	=	{ve gu}
{se xi vo gu}	=	{xe gu}
	...

{se xi ro gu P0 gi P1 gi ... gi Pn (gi'i)}

=

Pn

se xi ky gu bo A gi B gi C gi ...

	se xi ky gu bo P0 gi P1 gi ... gi Pn (gi'i)
=	se xi ky gu P0 gi P1 gi ... gi Pn (gi'i)
=	Pk

se xi ky gu nai A gi B gi C gi ...

In the case of k=0

	se xi no gu nai P0 gi P1 gi ... gi Pn (gi'i)
=	gu ¬P0 gi P1 gi ... gi Pn (gi'i)
=	¬P0

In the case of k≠0

	se xi ky gu nai P0 gi P1 gi ... gi Pn (gi'i)
=	se xi ky gu ¬P0 gi P1 gi ... gi Pn (gi'i)
=	Pk

se xi ky gu nai bo A gi B gi C gi ...

	se xi ky gu nai bo P0 gi P1 gi ... gi Pn (gi'i)
=	se xi ky gu ¬P0 gi ¬P1 gi ... gi ¬Pk gi ... gi ¬Pn (gi'i)
=	¬Pk